Beberapa Teori Dasar Dalam Artificial Intelegence

Teori MiniMax

Algoritma Minimax (juga sering disebut Minmax) adalah sebuah algoritma yang mendasari pola pikir langkah penyelesaian masalah dalam beberapa jenis permainan komputer, seperti tic-tac-toe, othello, checkers, catur, dll. Pada dasarnya, algoritma Minimax sangat andal untuk menyelesaikan segala masalah dalam pencarian langkah untuk permainan komputer dengan jumlah kemungkinan penyelesaian yang kecil, seperti pada permainan tic-tac-toe. Tetapi, jika algoritma Minimax digunakan pada permainan dengan jumlah kemungkinan penyelesaian yang besar seperti pada permainan catur, algoritma Minimax ini memerlukan waktu yang sangat lama untuk membangun pohon penyelesaian.

Dasar Teori Minimax

Secara teori, algoritma Minimax didefinisikan sebagai berikut: “Untuk setiap permainan satu-lawan satu, ada sebuah nilai yang bernilai V dan strategi yang dipilih oleh tiap pemain, sehingga: (a), Jika diberikan strategi dari pemain ke-2, maka langkah penyelesaian terbaik dari pemain pertama adalah V. Dan (b), jika diberikan strategi dari pemain pertama, maka langkah penyelesaian terbaik dari pemain kedua adalah –V” [6] Singkatnya, pemain pertama memberikan langkah penyelesaian yang bernilai V terhadap permainan pemain kedua, dan sebaliknya, pemain kedua memberikan langkah peyelesaian bernilai –V. Pemikiran inilah yang mendasari asal usul penamaan algoritma Minimax, dimana pemain yang satu berjuang untuk mendapat nilai maksimum,sedangkan lawannya berjuang untuk mendapat nilai minimum.

Langkah Membuat Teori Minimax

Langkah-langkah membuat algoritma Minimax adalah sebagai berikut:

1. Misalkan ada 2 pemain yang terlibat, kita namakan MAX dan MIN.
2. Lalu sebuah pohon pencarian dibangkitkan secara depth-first-search dari posisi awal permainan hingga akhir permainan.
3. Dari sudut pandang MAX, akan dicari posisi terakhir yang paling menguntungkan bagi MAX.

Contoh 1 Algoritma Minimax

MinMax (GamePosition game) {
	return MaxMove (game);
}
MaxMove (GamePosition game) {
if (GameEnded(game)) {
	return EvalGameState(game);
}
else {
	best_move < - {};
	moves <- GenerateMoves(game);
ForEach moves {
	move <- MinMove(ApplyMove(game));
if (Value(move) > Value(best_move)) {
	best_move < - move;
	}
}
return best_move;
	}
}

Contoh 2 Algoritma Minimax

MinMove (GamePosition game) {
	best_move <- {};
	moves <- GenerateMoves(game);
ForEach moves { 
	move <- MaxMove(ApplyMove(game));
if (Value(move) >Value(best_move)) {
	best_move < - move;
	}
}
return best_move;

Arti algoritma di atas : Yang terjadi pada algoritma diatas adalah, MAX akan mengambil nilai maksimum dari pohon pencarian yang dibangkitkan pada simpul terakhir. Sebaliknya, MIN akan menangkis serangan MAX dengan mengambil nilai minimum pada posisi akhir permainan, yang akan meminimalisasi serangan MAX.

Kelemahan Teori Minimax

Dengan membangkitkan pohon pencarian ini, komputerakan selalu mendapatkan penyelesaian terbaik untuksetiap langkahnya. Tetapi, masalah muncul ketika jumlah input yang dimasukkan menjadi banyak. Bayangkan saja, untuk posisi pertama dalam permainan catur dimana hanya terdapat kemungkinan untuk bergerak bagi 8 pion dan 2 kuda, akan terdapat sebanyak 82 + 22 = 20 kemungkinan. Hal ini berarti pada simpul awal akan didapatkan 20 sub-simpul sebagai langkah penyelesaian pada aras (level) ke 1. Jika komputer melakukan hal yang sama untuk menganalisis langkah selanjutnya (berarti komputer melakukan pembangkitan pohon untuk simpul pada aras ke 1) maka akan dilakukan 20 pembangkitan dimana pada tiap pembangkita akan dilakukan puluhan pembangkitan lain untuk aras ke 2. Demikian seterusnya hingga algoritma mencapai aras terakhir permainan, skakmat.

Contoh Kasus

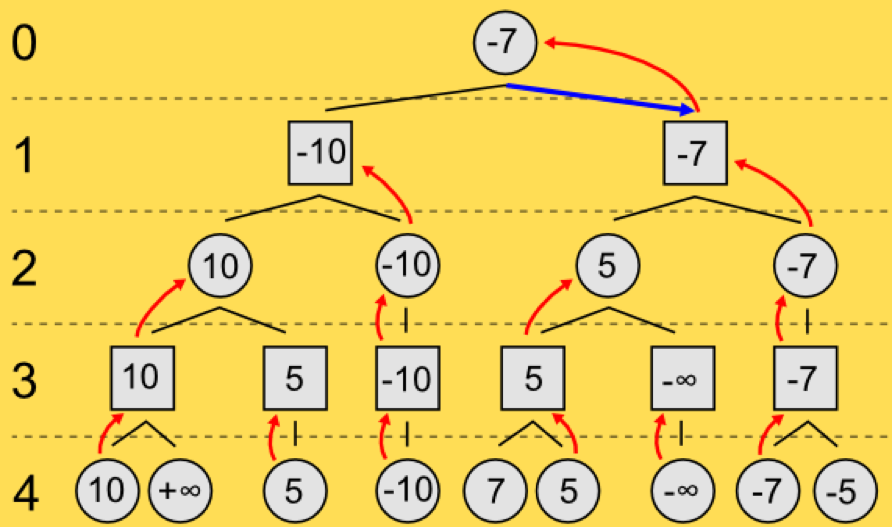
Teori Alpha – Betha Prunning

Dalam algoritma minimax, banyak terjadi kejadian dimana terjadi pengecekan sebuah simpul yang seharusnya tidak dicek karena tidak akan mempengaruhi hasil akhir. Untuk menghindari hal yang demikian, telah dibuat suatu algoritma minimax yang lebih optimal, yaitu algortima alpha beta pruning. Hasil algoritma alpha beta pruning sendiri tidak berubah dari algoritma minimax, yang berubah hanya traversalnya yang lebih sedikit. Cara kerja algoritma ini adalah dengan mengecek sebuah simpul n, dan jika pemain memiliki pilihan yang lebih baik pada akar n atau simpul-simpul selanjutnya, maka sebenarnya n tidak pernah dicapai pada waktu permainan. Maka pada n akan dilakukan pruning, yaitu simpul n tidak akan dikembangkan lagi pada pohon. Algoritma alpha beta pruning memanfaatkan dua nilai, yaitu alpha dan beta. Nilai alpha menunjukkan skor pilihan terbaik yang bisa diambil pemain Max, dan nilai beta menunjukan skor pilihan terbaik yang bisa diambil pemain Min. Pruning dilakukan ketika simpul yang sedang ditinjau pada pemain Max, yaitu n, memiliki skor yang lebih rendah daripada alpha, maka n tidak perlu ditinjau lagi berikutnya. Hal yang sama dilakukan pada pemain Min memakai nilai beta.

Contoh Kasus

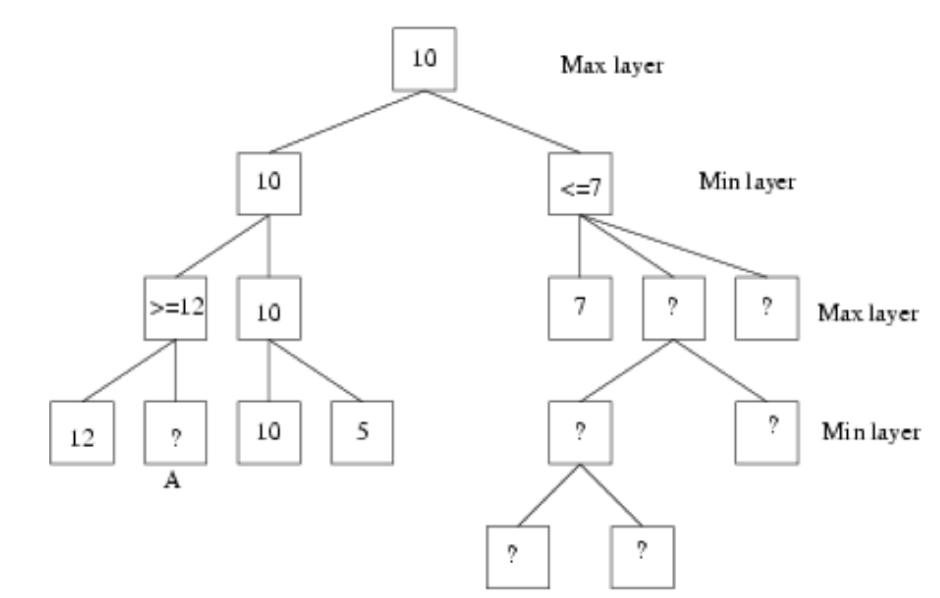
Seperti terlihat, nilai skor yang tidak ditinjau (dengan „?‟) tidak mempengaruhi nilai skor pada akar pohon keputusan. Coba lihat node A. Node ini tidak perlu dievaluasi karena pemain Min sudah mengambil keputusan di simpul bernilai 10. Ini disebut dengan beta-cutoff. Kemudian coba lihat node yang belum ditinjau di subpohon bagian kanan. Node-node ini juga tidak perlu dievaluasi karena pemain Max sudah mengambil keputusan di simpul bernilai 10 untuk mencegah pemain Min mengambil keputusan di simpul bernilai 7. Ini disebut dengan alpha-cutoff. Dengan kedua cutoff tadi, terlihat bahwa simpul yang perlu ditinjau dengan alpha beta pruning jauh lebih sedikit daripada jika kita memakai algoritma minimax biasa.

Teori Constraint Satisfaction Problem (SCP)

Constraint Satisfaction Problem (CSP) merupakan sebuah pendekatan dari problem yang bersifat matematis dengan tujuan menemukan keadaan atau obyek yang memenuhi sejumlah persyaratan atau criteria

Contoh Penerapan SCP

• Backtracking
• Forward checking
• Look Ahead
• Constraint propagation
• Arc and path consistency
• Variable and value ordering
• Hill climbing

Contoh Algoritma

Contoh Kasus

A crossword puzzle: We are to complete the puzzle

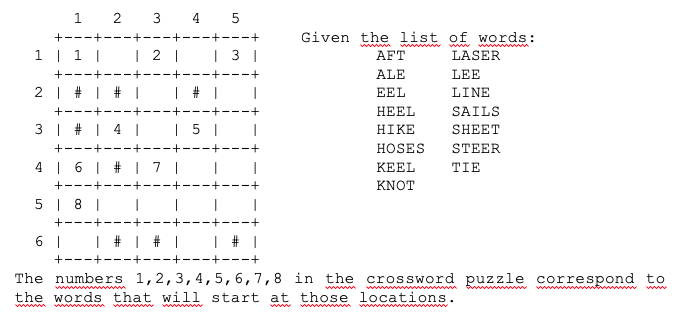
Latihan

1. Selesaikan criptarithmetic Problem berikut dengan algoritma Constrain Satisfaction :

   

   Jawab

   

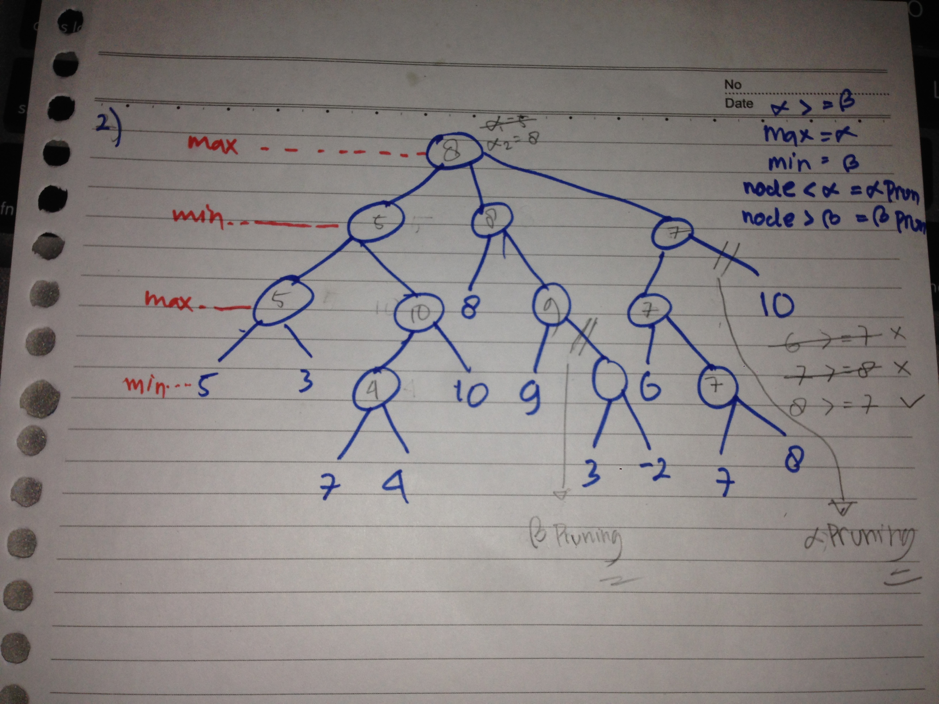
2. Di bawah ini diperlihatkan search tree dari suatu maximizing game. Dengan menggunakan alph beta prunning algoritm, tentukan nilai alpha optimal yang dapat dicapai oleh seorang maximizing player. Jelaskan bagaimana mekanisme cut off dilakukan terhdp cabang yang tidak relevan

   

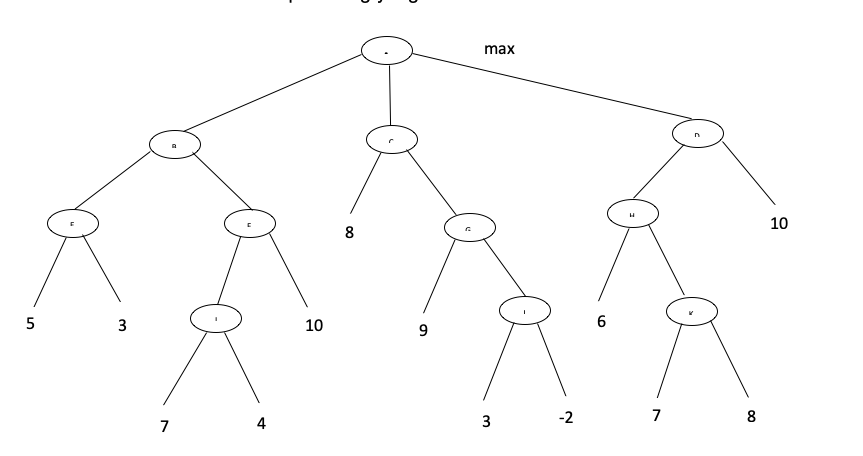
   Jawab